Lei de Coulomb (II)

4ª aula

Borges e Nicolau

Lei de Coulomb

A intensidade da força de ação mútua entre duas cargas elétricas puntiformes é diretamente proporcional ao produto dos valores absolutos das cargas e inversamente proporcional ao quadrado da distância que as separa.

k: constante eletrostática do meio onde estão as cargas.

No vácuo:

Exercícios básicos
 
Exercício 1:
Duas partículas eletrizadas com cargas elétricas Q e 4Q estão fixas em pontos A e B, situados a uma distância D. No ponto C, a uma distância d de A, coloca-se outra partícula eletrizada com carga elétrica q e observa-se que ela fica em equilíbrio sob ação de forças eletrostáticas somente. Determine a relação d/D.

Exercício 2:
Três partículas eletrizadas com cargas elétrica Q, 2Q e 3Q estão fixas nos pontos A, B e C, conforme a figura. Seja F a intensidade da força eletrostática que B exerce em C. Qual é, em função de F, a intensidade da força eletrostática que A exerce em C?

Exercício 3:
Três partículas eletrizadas, A, B e C, estão fixas nos vértices de um triângulo equilátero de lado L = 30 cm. Determine a intensidade da força eletrostática resultante da ação A e B sobre C. Analise os casos:

Dados: Q = 1,0 μC e k0 = 9.10⁹ N.m²/C²


Exercício 4:
Três partículas eletrizadas com cargas elétricas iguais a Q estão fixas nos vértices A, B e C de um quadrado. Uma quarta partícula eletrizada com carga elétrica q é fixada no vértice D. Para que a força eletrostática resultante sobre a partícula colocada em B seja nula, devemos ter:

a) q = Q
b) q = -Q
c) q = 2√2Q
d) q = -√2Q
e) q = -2√2Q


Exercício 5:
Seis partículas eletrizadas estão fixas nos vértices de um hexágono regular de lado
L = 30 cm, conforme mostra a figura. Sendo Q = 1 μC e k0 = 9.10⁹ N.m²/C², determine a intensidade da força eletrostática resultante que age numa partícula eletrizada com carga elétrica q = 10^-8 C, colocada no centro do hexágono.

Exercícios de Revisão

Revisão/Ex: 1
(UNICAMP-SP)
Cada uma das figuras abaixo representa duas bolas metálicas de massas iguais, em repouso, suspensas por fios isolantes. As bolas podem estar carregadas eletricamente. O sinal da carga está indicado em cada uma delas. A ausência de sinal indica que a bola está descarregada. O ângulo do fio com a vertical depende do peso da bola e da força elétrica devido à bola vizinha. Indique em cada caso se a figura está certa ou errada.

Revisão/Ex: 2
(UFAM)
Três corpos pontuais X, Y e Z têm cargas de mesma intensidade e sinais mostrados na figura. Elas estão localizadas em um triãngulo isósceles. As cargas X e Y são mantidas fixas e a carga Z é livre para se mover. Qual a direção e o sentido da força elétrica em Z?
As opções de direção e sentido estão listadas na própria figura.

Revisão/Ex: 3
(UFTM)
Duas esferas metálicas idênticas, de pequenas dimensões e isoladas, têm cargas elétricas positivas q₁ e q₂. O gráfico 1 representa a variação do módulo da força de repulsão entre elas, em função da distãncia que as separa.
Essas esferas são colocadas em contato, de modo que a carga total se conserve, e depois são separadas. O gráfico 2 representa a variação do módulo da força de repulsão entre elas, em função da distãncia que as separa, nessa nova situação.

Sabendo que k = 9.10⁹ N.m²/C², calcule:

a) O módulo da força F₁ indicada no gráfico 1.
b) O valor de q₁+q₂.


Revisão/Ex: 4
(UFTM)
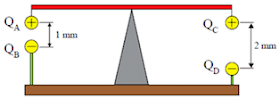
Uma haste isolante, homogênea e apoiada em seu centro geométrico equilibra quatro pequenas esferas idênticas e de massas desprezíveis, carregadas com cargas elétricas Q_A, Q_B, Q_C e Q_D, posicionadas como mostra a figura.

Se as intensidades das cargas elétricas Q_B, Q_C e Q_D são iguais a Q, a carga elétrica Q_A, para que seja mantido o equilíbrio horizontal da haste, é igual a

(A) Q/4.
(B) Q/2.
(C) Q.
(D) 2.Q.
(E) 4.Q.


Revisão/Ex: 5
(UEG)
Duas esferas idênticas são suspensas por fios de complimento l, com os pontos de suspensão separados por 2l. Os fios são isolantes, inextensíveis e de massas desprezíveis. Quando as esferas estão carregadas com cargas Q, de mesmo sinal, os fios fazem um ângulo de 30º com a vertical. Descarregando as esferas e carregando-as com cargas q de sinais opostos, os fios formam novamente um ângulo de 30º com a vertical. De acordo com as informações apresentadas, calcule o módulo da razão Q/q.




Exercícios básicos
 
Exercício 1: resolução

F_AC = F_BC => k₀.Q.q/d² = k₀.4Q.q/(D-d)² => 1/d = 2/(D-d) => d/D = 1/3

Resposta: d/D = 1/3

Exercício 2: resolução

F_BC  = F = k₀.2Q.3Q/d² (1)
F_AC  = k₀.Q.3Q/5d² (2)

De (1) e (2), vem: F_AC = F/10 

Resposta: F/10 

Exercício 3: resolução

a) F = k₀.Q.Q/L² => F = 9.10⁹.1,0.10^-6.1,0.10^-6/(0,30)² => F = 1,0.10^-1 N

cos 30º = (F_result/2)/F => √3/2 = (F_result/2)/1,0.10^-1 =>
F_result = 1,0.√3.10^-1 N

b) O triângulo indicado abaixo é equilátero. Logo, F_result = F = 1,0.10^-1 N

Respostas:
a) 1,0.√3.10^-1 N
b) 1,0.10^-1 N

Exercício 4: resolução

F = k₀.Q.Q/d² e F' = k₀.IqI.Q/(d√2)² => k₀.IqI.Q/2d²

Para que a força resultante sobre a partícula colocada em B seja nula, devemos impor que:
F' = F.√2 => k₀.IqI.Q/2d² = (k₀.Q.Q/d²).√2 => IqI = 2Q√2
q tem sinal oposto ao de Q. Logo, q = -2Q√2

Resposta: e

Exercício 5: resolução

F = k₀.Q.q/L² => F = 9.10⁹.10^-6.10^-8/(0,30)² => F = 10^-3 N
F_result = 4F = 4.10^-3 N

Resposta: 4.10^-3 N

Exercícios de Revisão

Revisão/Ex 1: resolução

(a) errada. As esferas têm sinais opostos e se atraem
(b) correta.
(c) errada. Não há repulsão. As esferas estão neutras.
(d) errada. Uma esfera eletrizada atrai uma neutra.
(e) errada. As esferas se repelem e os ângulos dos fios com a vertical são iguais.

Resposta: b

Exercícios de Revisão

Revisão/Ex 2: resolução

A esfera X atrai a esfera Z com força F_XZ e a esfera Y repele a esfera Z com força F_YZ. Estas forças têm mesma intensidade. A resultante tem a direção e o sentido de b).

Resposta: b

Revisão/Ex 3: resolução

a) Da lei de Coulomb, F = k.Iq₁I.Iq₂I/d², concluímos que triplicando d a intensidade da força fica dividida por 9. Portanto: F₁ = 20 N
 
b) Do gráfico 2: 
F = k.[I(q₁+q₂)/2I.I(q₁+q₂)/2I]/d² => 90 = 9.10⁹[(q₁+q₂)²/4]/3² =>
q₁+q₂ = 6.10^-4 C

Respostas: a) 20 N   b) 6,0.10^-4 C

Revisão/Ex 4: resolução

Para que seja mantido o equilíbrio horizontal da haste as forças de atração de B em A e de D em C devem ter as mesmas intensidades:
F_BA = F_DC =>
k.IQ_BI.IQ_AI/(1mm)² = k.IQ_DI.IQ_CI/(2mm)²
Sendo IQ_BI = IQ_CI = IQ_DI = Q, vem:
IQ_AI = Q/4 => Q_A = Q/4

Resposta: A

Revisão/Ex 5: resolução

Cargas Q de mesmo sinal:
T.sen 30º = k.Q²/D² e T.cos 30º = P => tg 30º = k.Q²/P.D² (1)
D = 2l+2l.sen 30º => D = 3l

Cargas q de sinais opostos:

T.sen 30º = k.q²/d² e T.cos 30º = P => tg 30º = k.q²/P.d² (2)
d = 2l-2l.sen 30º => d = l

(1) = (2) => Q²/D² = q²/d² => IQ/qI = D/d = 3l/l => IQ/qI = 3

Resposta: 3