OBF 2013 - link da resulação comentada - 2a fase

OBF 2a fase 2013 - Link da Resolução

Nível 1

Nível 2

Nível 3

Simulado de Óptica

Exercício 1:
(UFAM)

Um homem de altura y está a uma distância D de uma câmara de orifício de comprimento L. A sua imagem formada no interior da câmara tem uma altura y/20. Se duplicarmos a distância entre o homem e o orifício, a nova imagem terá altura:

 a) y/120  b) y/80  c) y/60  d) y/2  e) y/40

Resolução:

De i/o = p’/p, concluímos que dobrando p, i cai à metade. Portanto, de y/20 a imagem passa a ter altura y/40.

Resposta: e

Exercício 2:

(UESPI)

Uma bola vai do ponto A ao ponto B sobre uma mesa horizontal, segundo a trajetória mostrada na figura a seguir. Perpendicularmente à superfície da mesa, existe um espelho plano. Pode-se afirmar que a distância do ponto A à imagem da bola quando ela se encontra no ponto B é igual a:

A) 8 cm

B) 12 cm

C) 16 cm

D) 20 cm

E) 32 cm

Resolução:

Triângulo AB’C:

(AB’)² = (12)² + (16)² => AB’ = 20 cm

Resposta: D

Exercício 3:

(UFAM)

Um raio de luz, i, incide paralelamente ao eixo principal de um espelho côncavo de raio de curvatura de 60 cm. O raio refletido vai atravessar o eixo principal no ponto de abscissa, em cm, igual a:

a) 30   b) 10   c) 20   d) 60   e) 40

Resolução:

O raio refletido atravessa o eixo principal passando pelo foco principal e, portanto, a uma distância do espelho igual a R/2 = 30 cm.

Resposta: a

Exercício 4:

(Mackenzie-SP)

Um objeto real se encontra sobre o eixo principal de um espelho côncavo, de distância focal 10 cm, e a 20 cm do vértice do espelho. Sendo obedecidas as condições de Gauss, sua imagem é

a) real e direita.                                  b) real e invertida.

c) virtual e direita.                               d) virtual e invertida.

e) imprópria, localizada no infinito.

Resolução:

O objeto se encontra no centro de curvatura do espelho. Logo, a imagem formada é real, invertida e tem a mesma altura do objeto.

Resposta: b

Exercício 5:

(UNIFAL-MG)

Um objeto real, direito, situado no eixo principal de um espelho esférico côncavo, 20 cm distante do vértice do espelho, forma uma imagem real situada a 60 cm do vértice do espelho. Assinale a alternativa correta.

a) A imagem formada está entre o foco e o centro de curvatura.

b) A imagem formada é maior que o objeto e direita.

c) A distância focal do espelho é de 30 cm.

d) A imagem é menor que o objeto e invertida.

e) O objeto está situado entre o foco e o centro de curvatura do espelho.

Resolução:

Vamos determinar a distância focal do espelho aplicando a equação de Gauss:

1/f = 1/p + 1/p’ => 1/f = 1/20 + 1/60 => f = 15 cm.

Concluímos que o objeto está situado entre o foco e o centro de curvatura.

Resposta: e

Exercício 6:

(Unimontes-MG)

Um mergulhador, submerso em um lago, vê o Sol fazendo um ângulo de elevação aparente θ = 45º, com a superfície do lago. Seja α o ângulo de elevação real que o Sol faz com o horizonte, na situação descrita. O valor de [sen(α)]² é, aproximadamente,

Dados:

Índice de refração do ar = 1,00

Índice de refração da água = 1,33

sen 45º ≅ 0,710

sen (90º - x) = cos (x)

A) 0,389

B) 0,554

C) 0,412

D) 0,108

Resolução:

Lei de Snell-Descartes:α 
n₁.sen i = n₂.sen r 
1.sen (90º - α) = 1,33.sen 45º
cos α = 1,33.0,710
cos α ≈ 0,944
[sen (α)]² = 1 - [cos (α)]²
[sen (α)]² ≈ 0,108

Resposta: D

Exercício 7:
(UFRR)
A figura mostra um material, em formato de quadrado, com índice de refração desconhecido. No canto direito, inferior, do quadrado, emerge um feixe de luz. A luz atravessa a diagonal do quadrado e sai pelo seu canto esquerdo, superior, de modo que a direção de propagação da luz no ar (cujo índice de refração é aproximadamente igual a 1) seja paralela ao lado superior do quadrado. Nestas condições:

A) O índice de refração do material é 0,707.
B) O índice de refração do material é √2/2
C) O índice de refração do material é √2
D) O índice de refração do material é 0,5
E) O índice de refração do material é 2

Resolução:

Como o raio emerge rasante, concluímos que o ângulo de incidência é o ângulo limite, isto é, L = 45º
Sendo sen L = 1/n, vem: sen 45º = 1/n => n = 1/sen 45º =>
n = 1/(√2/2) => n = √2

Resposta: C
 
Exercício 8:
(UFES)

Para que ocorra reflexão total em uma fibra óptica, é necssário que

A) o índice de reflexão do núcleo seja igual ao do revestimento
B) o índice de refração do núcleo seja igual ao do revestimento
C) o índice de reflexão do núcleo seja maior que o do revestimento
D) o índice de refração do núcleo seja maior que o do revestimento
E) o índice de refração do núcleo seja menor que o do revestimento

Resolução:

Na fibra óptica a luz sofre reflexão total. Para que tal ocorra o índice de refração do núcleo deve ser maior do que o do revestimento. Além disso, o ângulo de incidência deve ser maior do que o ângulo limite.

Resposta: D

Exercício 9:
(UFU-MG)
A figura abaixo representa um feixe de luz branca viajando pelo ar e incidindo sobre um pedaço de vidro crown. A tabela apresenta os índices de refração (n) para algumas cores nesse vidro.

Nesse esquema o feixe refratado 3 corresponde à cor

A) branca
B) violeta
C) verde
D) vermelha

Resolução:

O índice de refração do vidro para a luz violeta é maior do que para as demais cores. Logo, a luz violeta é a que mais se aproxima da normal. Portanto, no esquema apresentado o feixe refratado 3 corresponde à luz violeta.

Resposta: B

Exercício 10:
(UECE)
Um raio de luz propagando-se no ar incide, com um ângulo de incidência igual a 45º, em uma das faces de uma lâmina feita com um material transparente de indice de refração n, como mostra a figura.

Sabendo-se que a linha AC é o prolongamento do raio incidente, d = 4 cm e
BC = 1 cm, assinale a alternativa que contém o valor de n.

A) 2√3
B) 5√2/6
C) 3√3/2
D) 1,5

Resolução:

O triângulo AOC é retângulo e isósceles. Logo, OC = d = 4 cm.
Portanto, OB = 4 cm – 1 cm = 3 cm.
Pelo Teorema de Pitágoras, temos: AB= 5 cm. 

Pela Lei de Snell-Descartes:

n_ar.sen i = n.sen r => 1.sen 45º = n.(OB/AB) =>
 √2/2 = n.(3/5) => n = 5.√2/6

Resposta: B

Exercício 11:
(UTFPR)
Um objeto é colocado frente ao sistema óptico representado abaixo. Esboce a imagem formada:

Assinale as alternativas abaixo com V se verdadeira ou F se falsa.

(  ) A formação da imagem esquematizada é comum nas câmeras fotográficas.
(  ) A imagem é invertida, maior e pode ser projetada num anteparo.
(  ) A imagem forma-se geometricamente entre o foco imagem e o ponto antiprincipal.

A sequência correta será:

A) V, F, V
B) V, F, F
C) F, V, F
D) F, F, F
E) V, V, F

Resolução:

I) Falsa. Nas câmaras fotográficas o objeto está localizado antes do ponto antiprincipal objeto A.
II) Verdadeira. A imagem é real, invertida  e maior do que o objeto. Sendo real pode ser projetada num anteparo
III) Falsa. A imagem forma-se depois  do ponto antiprincipal imagem A’.

Resposta: C

Exercício 12:
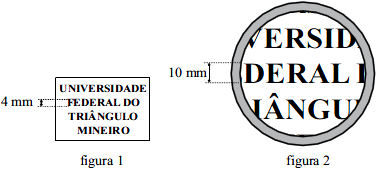
(UFTM)
As figuras mostram um mesmo texto visto de duas formas: na figura 1 a olho nu, e na figura 2 com auxílio de uma lente esférica. As medidas nas figuras mostram as dimensões das letras nas duas situações.

Sabendo que a lente foi posicionada paralelamente à folha e a 12 cm dela, pode-se afirmar que ela é


(A) divergente e tem distância focal -20 cm
(B) divergente e tem distância focal -40 cm
(C) convergente e tem distância focal 15 cm
(D) convergente e tem distância focal 20 cm
(E) convergente e tem distância focal 45 cm

Resolução:

A imagem é direita e maior do que o objeto. Logo, trata-se de uma lente convergente.
i/o = -p’/p => 10/4 = -p’/12 => p’ = -30 cm.
1/f = 1/p + 1/p’ => 1/f = 1/12 + 1/(-30) => f = + 20 cm.
O fato de a distância focal ser positiva, confirma que a lente é convergente.

Resposta: D

Exercício 13:
(PUC-PR)
A equação de Gauss relaciona a distância focal (f) de uma lente esférica delgada com as distâncias do objeto (p) e da imagem (p’) ao vértice da lente. O gráfico dado mostra a distância da imagem em função da distância do objeto para uma determinada lente. Aproximadamente, a que distância (p) da lente deve ficar o objeto para produzir uma imagem virtual, direita e com ampliação (m) de 4,0 vezes?

A) 10 cm
B) 20 cm
C) 8,0 cm
D) 7,5 cm
E) 5,5 cm

Resolução:

Do gráfico, para p = 20 cm, temos p’ = 20 cm.

Pela equação de Gauss calculamos a distância focal:
 
1/f = 1/p + 1/p’ => 1/f = 1/20 + 1/20 => f = 10 cm
 
Aumento linear transversal:
 
i/o = -p’/p => 4,0 = -p’/p => p’ = -4,0 p
1/f = 1/p + 1/p’ => 1/10 = 1/p + 1/(-4,0 p) => p = 7,5 cm

Resposta: D

Exercicio 14:
(UFAM)
Um objeto retilíneo de 4 cm é colocado transversalmente ao eixo principal de uma lente esférica convergente. A distância entre o objeto e o centro da lente vale 36 cm. A distância focal da lente vale 12 cm. A amplificação e o tamanho da imagem valem respectivamente:

a)  -0,50 e - 2 cm (invertida)
b)  -0,75 e - 2 cm (invertida)
c)  -0,25 e – 2 cm (invertida)
d)  0,50 e 2 cm (direita)
e)  0,75  e  2 cm (direita)

Resolução:

Equação de Gauss:

1/f = 1/p + 1/p’ => 1/12 = 1/36 + 1/p’ => p’ = 18 cm
A = -p’/p => A = -18/36 => A = -0,50 (imagem invertida)
A = i/o => -0,50 = i/4 => i = -2 cm

Resposta: a

Exercício 15:
(UFPE)
Um objeto de altura h = 2,5 cm está localizado a 4,0 cm de uma lente delgada de distância focal f = +8,0 cm. Determine a altura deste objeto, em cm, quando observado através da lente.

A) 3,0
B) 4,5
C) 5,0
D) 6,5
E) 2,5

Resolução:

Equação de Gauss:

1/f = 1/p + 1/p’ => 1/8,0 = 1/4,0 + 1/p’ => p’= -8 cm

Aumento linear transversal:

i/o = -p’/p => i/2,5 = -(-8)/4 => i = 5,0 cm

Resposta: C

Exercício 16:
(VUNESP-SP)
Para que alguém, com o olho normal, possa distinguir um ponto separado de outro, é necessário que as imagens desses pontos, que são projetadas em sua retina, estejam separadas uma da outra a uma distância de 0,005 mm.

Adotando-se um modelo muito simplificado do olho humano no qual ele possa ser considerado uma esfera cujo diâmetro médio é igual a 15 mm, a maior distância x, em metros, que dois pontos luminosos, distantes 1 mm um do outro, podem estar do observador, para que este os perceba separados, é:

a) 1. b) 2. c) 3. d) 4. e) 5. 

Resolução:

Considerando retilínea a imagem que se forma na retina
(de comprimento 0,005 mm), pela semelhança entre os triângulos formados, obtemos:

x/15 mm = 1 mm/0,005 mm => x = 3000 mm = 3 m

Resposta: c

Exercício 17:
(UFSCAR-SP) 
... Pince-nez é coisa que usei por largos anos, sem desdouro. Um dia, porém, queixando-me do enfraquecimento da vista, alguém me disse que o mal talvez viesse da fábrica. ...

(Machado de Assis, Bons Dias, 1888.)

Machado de Assis via-se obrigado a usar lentes corretivas que, em sua época, apoiavam-se em armações conhecidas como pince-nez ou lorgnon, que se mantinham fixas ao rosto pela ação de uma débil força elástica sobre o nariz. 
Supondo que Machado, míope, só conseguisse ver nitidamente objetos à sua frente desde que estes se encontrassem a até 2 m de seus olhos, e que ambos os olhos tivessem o mesmo grau de miopia, as lentes corretivas de seu pince-nez deveriam se de vergência, em dioptrias,


a) +2,0.     b) -0,5.     c) -1,0.
d) - 1,5.     e) -2,0.

Resolução:

A distância do ponto remoto ao olho era de 2 m. Logo, a distância focal das lentes divergentes corretivas era f = -2 m. Sendo a vergência o inverso da distância focal, vem:

V = 1/f = 1/-2 => V= -0,5 di

Resposta: b
 

Classificados para a OBF 2013 - 2 Fase

Pontuação para a 2ª fase da OBF 2013 Os estudantes que atingiram, na Prova da 1ª Fase, o número de pontos indicado abaixo estão automaticamente inscritos para a 2ª Fase da OBF 2013:

» 8º ano: 6 (SEIS) pontos – Ensino Fundamental (NÍVEL I)
» 9º ano: 7 (SETE) pontos – Ensino Fundamental (NÍVEL I)
» 1ª série: 7 (SETE) pontos– Ensino Médio (NÍVEL II)
» 2ª série: 8 (OITO) pontos– Ensino Médio (NÍVEL II)
» 3ª e 4^a séries: 8 (OITO) pontos– Ensino Médio/Ensino Técnico (NÍVEL III)

O Regulamento da OBF 2013, no item 4.1 assegura que: A escola que participar da 1ª fase terá automaticamente inscritos para a 2ª fase todos os estudantes que atingirem o número mínimo de acertos estipulado pela Comissão da OBF. As provas da 2ª fase serão aplicadas no dia 10 de agosto de 2013, sábado, das 13h às 17h (horário local), nas sub-coordenações estaduais definidas por cada comissão estadual.

ATIVIDADES PARALELAS OBF 2013: Todos os alunos inscritos na OBF 2013 podem participar.

Parabéns a Todos os Classificados

9° Série

 

AMANDA ERI ANZE

 AMANDA LAIS M P PASCUAL

ANGELO DOMINGO MOURA

 BIANCA AZEDO GUIMARÃES

BRUNA SOUZA DO ROSÁRIO

CECILIA TIZATTO BARROSO

CLAUDIO QUEIROZ GUIMARÃES

CLEYTON RAPHAEL

FERNANDO AUGUSTO TEIXEIRA SILVA

GABRIEL FERNANDES BARBOSA

 GABRIELA CAMPOS COUTINHO

GLENDA REIS GUEDES DE MOURA

HEITOR TORRES GARRIDO

HENRIQUE BACELAR DE FARIAS

JOÃO LUCAS FURTADO

JOÃO PAULO T S MENDES

JOÃO PEDRO MENEZES LAUAND

JORGE MIGUEL S CABRAL

LEONARDO AYUB

LLAURA RIBEIRO AREF KZAM

LUCAS BASILIO SIMONETTI CABRAL

LUCCA DE ALMEIDA BENIGNO

LUIZA PAULA ROBERTO

MARIA EDUARDA DIAS DA COSTA

MARIA LUIZA VIDAL

NAYUMI TOYODA FONTES

PABLO ROBERTO SILVA MARQUES

PEDRO HENRIQUE FONSECA DE OLIVEIRA

PEDRO HENRIQUE VIEIRA

RAYANNA SIMÕES E SOUZA

ROBERTO NETO

ROBERTO VICTOR CARVALHO

THAÍSA DE SOUZA GALVÃO

VICTOR RAFAEL ORDOZGOITE

VICTORIA DE CASTRO CANTE PIMENTEL

VITOR MONTALVÃO TAVARES 

1° Ano do Ensino Médio

ADILTON CORREA GENTIL FILHO

ADRIAN BARREIROS DE SOUZA

ANA LUIZA ANDRADE DE SOUSA

BEATRIZ CAVALCANTE CARVALHO

BEATRIZ MELLA SOARES PÊSSOA

BRENDA MANUELY CONTO SIQUEIRA

CAROLINA DE OLIVEIRA E CASTRO

EDSON RAFAEL ZERBINATO MARTINS

FERNANDO HENRIQUE DE ARAUJO MAGALHÃES

GABRIEL CONTE CORTEZ MARTINS

GABRIELLE FABAR SANTOS

GRAZIELA ARAUJO MELO

GUSTAVO MACHADO RENDA

JOÃO PAULO ALFREDO CARVALHO DA COSTA

 LEONARDO BORGE MORAES

LEONARDO MATHEUS CANDIDO

LETÍCIA INGRID RAMOS ROSSY

LUANY CRISTINE SOUZA EGAS

LUCAS MARTINS DA SILVA

LUIZ CARLOS FERRAZ BARBOSA NETO

LUIZ TONIOLLI JUNIOR

MATHEUS CHAVES CALDAS

NICOLAS BABILONIA CAVALCANTI

PAULO HENRIQUE DIAS DA SILVA

ROGÉRIO FRAXE TAVARES

RUI NETO

SARAH DA SILVA SILVEIRA

STANLEY QUEIROZ FORTES NETO

THAINA BENTES MENDONCA

THAISE FARIAS RODRIGUES

VITOR SANTOS CORTEZ

YURI MORENO

 

2° Ano do Ensino Médio

ALGENOR MARIA DA COSTA TEIXEIRA NETO

ANA CAROLINA FREITAS TOYODA

ANA CAROLINA QUEIROZ CANDIDO DA SILVA

ANA VITORIA DO NASCIMENTO

ANDRÉ LUIZ BARROS DA SILVA NOGUEIRA

ARTUR GABRIEL DE SOUZA ROCHA

CAMILA BEATRIZ FRANKLIN DIAS

CARLOS HENRIQUE MESQUITA PERES

EDUARDO HENRIQUE CARVALHO DE CASTRO

EVELYN STEFFI AMPARO DA COSTA HURTADO CAVALCANTE

FERNANDA RODRIGUES MOLLES

GABRIEL MACEDO DE ALMEIDA

GABRIEL PACIFICO SEABRA NUNES

GABRIELA SILVA LEITE

GIOVANNA PAULA MACEDO DE LACERDA GUEDES

HENRIQUE PESSOA ARMOND DE MELO

HISSA RENATO CHAMMA

ICARO ZURRA VASCONELOS

ISABELLE LOUISE DA CRUZ LOPO DE FIGUEIREDO

IZABELA ZANOTTO MONTEIRO

JULIA CAROLLINE GUERRA BARBOSA

JULIA CRISTINA DE SOUZA ALVES

KARLLEN PORTELA CORREA

LARISSA OKADA ARAUJO

LIGIA REBECCA MOTA AMORIM

LORENA JEZINI LIMA

LUCAS FLORENCIO SANTOS ROCHA

LUCAS RAMOS NOBRE

MARCOS VINICIUS DE CASTRO FERREIRA

MARIA GIOVANA QUEIROZ DE LIMA

MARIA HELENA TUMA BESSA

MARIAH SOBREIRA LOIO LOUREIRO

MARIANNA DE LIMA FREITAS

MYLENA MIKI LOPES IDETA

PAULA ELWING TORRES

RAFAEL ALENCAR MATIAS

RAFAEL SANTIAGO SERRA PINTO

RAMEL CERDEIRA WEBER

RAQUEL MARIA DE MORAIS PEREIRA

REBECA NAVARRO DANTAS

RICARDO PINHEIRO FERNANDES LAGES

RODRIGO VASQUEZ DAN LINS

SARA MOREIRA DE ANDRADE

THIAGO CAVALCANTE PERREIRA

THIAGO COBRA E MONTEIRO

VICTOR DE MELO PINHEIRO

WALTER AMAZONAS TAVOLA DA SILVA

3° Ano do Ensino Médio

 

CAIO DE SOUZA CÂMARA

FELIPE GUEDES DE OLIVEIRA KUCERA

GABRIEL LUCAS ANDRADE DE SOUSA

JACOBUS LAURENS DE JAGER

JONAS PEREIRA FALCÃO

JUAN EDUARDO RIOS RODRIGUEZ

LUCAS HIAGO VARELA

NATAN LOPES DA CUNHA FILHO

VANESSA LEITE

9º Ano = 36
1ª série = 32
2ª série = 47
3ª série = 9
Total = 124