Dioptro Plano. Dispersão luminosa

Borges e Nicolau

Dioptro plano

É um sistema constituído de dois meios homogêneos e transparentes separados por uma superfície plana.
Por exemplo, a água tranquila de um tanque e o ar, separados pela superfície plana da água.
Vamos determinar as características da imagem P’ vista por um observador situado no ar, de um ponto objeto P localizado na água.

Note que a imagem é virtual, situa-se do mesmo lado do objeto e está mais próxima da superfície de separação S. Por isso, por exemplo, uma piscina aparenta ser mais rasa do que realmente é.
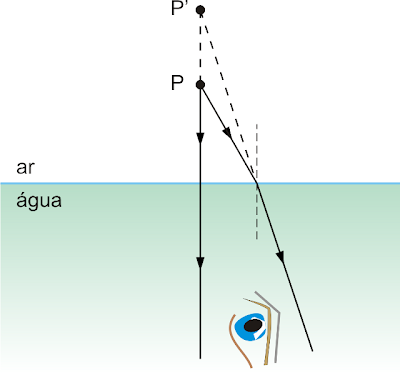
Veja, agora, como se obtém o ponto imagem P’, de um objeto P situado no ar, visto por um observador na água:

Dados os índices de refração dos meios (n e n’) e a distância d do ponto objeto P à superfície S é possível calcular a distância d’ do ponto imagem P’ à superfície S, pela equação de Gauss para os dioptros planos. Esta equação é válida quando os ângulos de incidência e refração são pequenos (até cerca de 10º)

n: índice de refração do meio onde está o objeto P.
n’: índice de refração do meio onde está o observador.

Na foto abaixo observamos a imagem de um objeto real fornecida por uma lâmina de vidro de faces paralelas. A lâmina é a associação de dois dioptros planos paralelos: ar/vidro e vidro/ar.

Se as superfícies de separação entre os dois dioptros não forem paralelas, no lugar da lâmina temos um prisma. Observe a foto abaixo:

Dispersão da luz

Um feixe de luz solar incide na face de um prisma. Este feixe se decompõe nos diversas componentes que constituem a luz policromática. Note que a componente que mais se desvia é a violeta e a que menos se desvia é a vermelha. Isto ocorre por que o índice de refração do vidro para a luz violeta é maior do que para a luz vermelha. Entre estas duas componentes temos as cores intermediárias. É a decomposição ou dispersão da luz.

Foto: Prova UEG-GO

Exercícios básicos

Exercício 1:
Um lápis, cuja ponta é indicada por P, é mergulhado num copo contendo água. Um observador situa-se na vertical que passa por P. Obtenha, utilizando dois raios de luz, a imagem P’ de P, vista pelo observador. Complete o desenho da parte do lápis imersa na água, o que dá a impressão de estar quebrado para cima.

Exercício 2:
Uma pessoa observa uma formiga F através de uma lâmina de faces paralelas. Obtenha a imagem F’ vista pela pessoa.

Exercício 3:
Um peixe encontra-se a 1,6 m de profundidade. Um pescador situa-se aproximadamente na vertical que passa pelo peixe. A que distância da superfície o pescador vê o peixe? Esta distância é chamada profundidade aparente.
Dados: índice de refração absoluto da água 4/3; índice de refração absoluto do ar 1,0.


Exercício 4:
Um pássaro encontra-se a 1,8 m de altura, em relação à superfície S que separa o ar da água de um lago. Um mergulhador na água situa-se aproximadamente na vertical que passa pelo pássaro. A que distância da superfície S o mergulhador vê o pássaro? Esta distância é chamada altura aparente.
Dados: índice de refração absoluto da água 4/3; índice de refração absoluto do ar 1,0.


Exercício 5:
Um feixe de luz policromática, constituído pelas cores amarelo, verde e azul, incide um prisma de vidro e sofre decomposição, conforme indica a figura.

As componentes A, B e C, são respectivamente:

a) Azul, amarela e verde;
b) Amarela; azul e verde;
c) Amarela, verde e azul;
d) Azul; verde e amarela;
e) Verde; amarela e azul.

Exercício 1: resolução

Exercício 2: resolução

Exercício 3: resolução
Equação de Gauss para os dioptros planos.

n/d = n'/d'

Sendo :
d = 1,6 m (profundidade real do peixe);
d’: profundidade aparente do peixe;

n = 4/3: índice de refração do meio onde está o peixe.
n’ = 1: índice de refração do meio onde está o observador (pescador).

Temos: (4/3)/1,6 = 1/d' => d' = 1,2 m

Resposta: 1,2 m

Exercício 4: resolução
Equação de Gauss para os dioptros planos.

n/d = n'/d'

Sendo :
d = 1,8 m (altura real do pássaro);
d’: altura aparente do pássaro;

n = 1: índice de refração do meio onde está o pássaro.
n’ = 4/3: índice de refração do meio onde está o mergulhador.

Temos: 1/1,8 = (4/3)/d' => d' = 2,4 m

Resposta: 2,4 m

Exercício 5: resolução
A componente que sofre o maior desvio é a azul. Logo C é a componente azul.
A componente que sofre o menor desvio é a amarela. Logo A é a componente amarela.
A componente verde sofre um desvio intermediário entre as duas anteriores (B).

Resposta: c