Capa do álbum "The Dark Side of The Moon"
Capa do álbum "The Dark Side of The Moon"
Neste
mês de março de 2013, o histórico vinil "The Dark Side of The Moon" da
banda Pink Floyd, lançado em 1973, completa 40 anos.
A capa da
obra musical nos remete a um belíssimo e conhecido fenômeno óptico: a
dispersão da luz branca nas faixas (ou frequências) do espectro visível.
E o título do álbum também nos faz lembrar de outra ideia importante na
Física e na Astronomia: a coincidência nos valores do período de
rotação da Lua (ao redor de si mesma) e o período orbital da própria Lua
(ao redor da Terra).
Aproveito o aniversário deste histórico álbum para (como sempre!) discutir Física.
:: A dispersão da luz branca
Chamamos
de luz branca à radiação luminosa (eletromagnética) composta pela
mistura de todas as cores visíveis que vão do vermelho ao violeta.
Isaac
Newton (1643-1727), bastante conhecido pelo seu trabalho com Mecânica e
Gravitação, também dedicou-se à Óptica. Em 1704 ele publicou as suas
ideias sobre a luz no livro "Opticks". Usando um prisma, Newton mostrou
que é possível separar as faixas constituintes da luz solar (branca),
mais ou menos como mostra a capa do álbum da banda Pink Floyd. Num
segundo momento, usando outro prisma (invertido em relação ao primeiro),
Newton mostrou que é possível juntar as cores novamente para
reconstituir a luz branca.
Quando a luz atravessa de um meio
material para outro (Refração), sabemos que se a incidência é oblíqua
(não perpendicular à superfície de separação dos meios), há mudança na
direção de propagação da luz. Se a luz passa do ar para o vidro
1
(do prisma), como no experimento de Isaac Newton e também na ilustração
da capa do álbum "The Dark Side os The Moon", cada cor sofre um desvio
diferente que aumenta do vermelho para o violeta. Da mesma forma,
observamos que há mudança na velocidade de propagação da luz que no
vidro é sempre menor que no ar e também tem valores diferentes para cada
cor sendo maior para o vermelho e menor para o violeta. A ilustração
abaixo nos mostra o sentido de aumento/diminuição da velocidade e do
desvio para as sete diferentes faixas de cores. Repare bem que a cor
que tem maior velocidade sofre menor desvio e vice-versa.

Para
efeito didático, é comum subdividirmos a faixa visível em sete faixas
distintas de cor: vermelho, alaranjado, amarelo, verde, azul (claro),
azul (anil ou escuro) e violeta. Mas cuidado: não existem apenas sete
cores! Na prática são infinitas cores visíveis. A ilustração da capa do
disco mostra apenas seis faixas monocromáticas (em vez de sete)
separadas após a luz passar pelo prisma. O desenhista ignorou a faixa do
azul escuro (ou azul anil). E em cada faixa a cor é única, sem tons
intermediários. São dois deslizes físicos que podemos ver em detalhe na
imagem abaixo, em zoom.
 Zoom na capa: apenas sei cores "chapadas", sem tons intermediários
Zoom na capa: apenas sei cores "chapadas", sem tons intermediários
Na
realidade, em cada uma das sete faixas de cor, do vermelho ao violeta,
devemos ter tons intermediários. Isso porque não existe apenas um tom de
vermelho "chapado". O vermelho começa escuro e vai "clareando",
tornando-se cada vez mais alaranjado. É difícil saber com certeza quando
termina o vermelho e começa o alaranjado. Com as outras cores ocorre o
mesmo e temos tons intermediários. Por isso mesmo, a melhor maneira de
estabelecermos uma fronteira entre as cores é falarmos em frequência (ou
comprimento de onda) da luz. Medindo a frequência (ou o comprimento de
onda), podemos estabelecer limites quantitativos para cada uma das sete
faixas da luz visível.
Uma representação
correta da dispersão da luz branca num prisma deve ser como nos mostra a
ilustração abaixo onde, para cada uma das sete faixas, temos infinitos
tons, como num arco-íris que também tem a ver com a separação das cores
da luz solar (branca) por gotas de água na atmosfera que atuam como
prismas dispersores .
 O que ocorre de fato: vários tons em cada uma das sete faixas de cores
O que ocorre de fato: vários tons em cada uma das sete faixas de cores
E
se você ainda está se perguntando qual a razão da dispersão da luz ser
bastante evidente num prisma, a reposta é simples: no prisma acontecem
duas refrações, uma na entrada da luz e outra na saída. A primeira
refração separa as cores um pouquinho. A segunda refração atua como
reforço da primeira, separando as cores um pouco mais. Numa única
refração, quase sempre é difícil perceber a separação de cores que tende
a ser sutil. Mas com duas refrações sucessivas, o fenômeno fica bem
evidente.
:: A Lua tem mesmo um lado escuro (dark side)?
A resposta é não! A Lua tem um lado oculto, mas não necessariamente escuro. Não consegue perceber a diferença? Explico.
A
Lua não tem luz própria. Ela é iluminada pelo Sol. Como o Sol está
sempre iluminando apenas um lado da Lua, nosso satélite tem sempre
metade da esfera iluminada (ou clara) e a outra metade escura, como na
figura abaixo.
Com
a Terra ocorre o mesmo. A Terra também é uma esfera opaca, maior do que
a Lua, mas iluminada pelo Sol. Sua face voltada para o Sol é sempre
clara. É dia para quem está nesta porção iluminada pelo Sol. A face
oposta ao Sol é sempre escura. E quem nela está experimenta a escuridão
da noite.
Conforme os dias vão passando, a Lua vai girando (em
movimento de rotação) ao redor de si mesma enquanto, simultaneamente,
também vai mudando de posição em sua órbita ao redor da Terra (em
movimento de translação). O que veremos da Lua daqui da Terra depende da
sua posição em relação a nós e também ao Sol. A próxima figura (fora de
escala) ilustra melhor esta ideia:
Podemos interpretar o que mostra a figura acima como:
- Lua Cheia,
que corresponde à metade iluminada da Lua integralmente voltada para
nós na Terra. Vemos a face da Lua voltada para nós integralmente clara;
- Quarto2 Minguante,
quando a face voltada para nós tem metade iluminada e metade escura.
Mas a porção clara está diminuindo gradativamente com o passar dos
dias (a Lua está indo da fase Cheia para a Nova);
- Lua Nova,
que corresponde à metade não iluminada (ou escura) da Lua voltada para
nós. Vemos a face da Lua voltada para nós integralmente escura;
- Quarto2 Crescente,
quando a face voltada para nós tem metade iluminada e metade escura.
Mas a porção clara está aumentando gradativamente com o passar dos
dias (a Lua está indo da fase Nova para a Cheia);
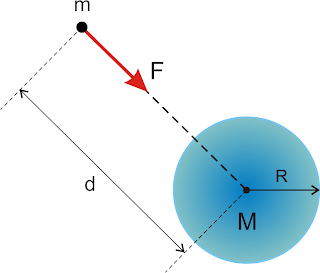
E tem um
outro detalhe crucial nessa história: curiosamente, com o passar do
tempo, a interação gravitacional entre a Terra e a Lua fez com que o
período (ou tempo) de rotação da Lua ao redor de si mesma ficasse igual
ao período (ou tempo) de translação ao redor da Terra. Assim, enquanto
gira ao redor de si mesma, a Lua translada ao redor do nosso planeta e
vai nos mostrando sempre a mesma face. Temos sempre a mesma metade da
Lua voltada para a Terra e por isso mesmo sempre vemos a mesma face da
Lua. A outra metade, a que nunca vemos daqui da Terra, é chamada de face
oculta.
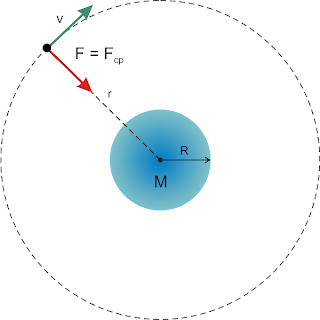
Para entender melhor como é isso, veja a imagem a
seguir (fora de escala) na qual marquei um ponto vermelho e outro verde
(em posições diametralmente opostas na esfera da Lua). Ambos giram ao
redor do centro da Lua por conta da rotação do nosso satélite. Quando a
Lua tiver dado uma volta completa na Terra, perfazendo o caminho
1-2-3-4-1, estes dois pontos deram uma volta completa ao redor do centro
da Lua. Em outras palavras, enquanto os pontos vermelho e verde giram, a
Lua vai mudando de lugar na sua órbita ao redor da Terra. Como o tempo
de rotação da Lua ao redor de si mesma é igual ao tempo de translação da
Lua ao redor da Terra, o ponto vermelho sempre está voltado para a
Terra e o ponto verde sempre estará na posição diametralmente oposta. O
ponto vermelho é o centro da face da Lua sempre apontada para a Terra. E
o ponto verde é o centro da face da Lua que nunca conseguimos ver daqui
da Terra, independente da posição da Lua em relação ao nosso planeta.

Repare
na imagem acima que o ponto verde, sempre oculto, pode estar num lado
claro (iluminado) ou escuro (não iluminado) da Lua. Ele sempre estará
numa posição em que nos é impossível vê-lo daqui da Terra. Logo, ele
está na face oculta da Lua. Mas ele pode estar ou não iluminado pelo
Sol. Logo, face oculta (impossível de ser vista da Terra) e face escura
(sem luz solar) são duas coisas bem diferentes. Deu para perceber?
A
mesma coisa acontece com o ponto vermelho, centro da face da Lua sempre
visível para nós daqui da Terra. Este ponto pode estar na região
iluminada ou não pelo Sol. E por isso temos as fases da Lua que nada
mais são do que a variação na proporção entre a região clara e a região
escura da face da Lua que está sempre voltada para a Terra, a face não
oculta.
_________________
Encerro este texto
ratificando que a bela e marcante capa do álbum "The Dark Side of The
Moon" contém alguns erros conceituais de Física. Mas a obra musical
original é das boas! Recomendo uma audição atenta, especialmente depois
deste passeio pela Física.
(1) Diferentes
materiais têm diferentes índices de refração absoluto (n), número que
caracteriza o meio opticamente e é obtido por n = c/V onde c é a
velocidade da luz no vácuo e V a velocidade da luz no meio.
(2) Cada
metade da esfera lunar (iluminada ou escura) pode ser chamada de metade
ou meio (1/2). Quando temos uma metade dividida novamente ao meio, sendo
uma parte clara e outra escura, então temos metade da metade, ou seja,
um quarto (1/4). O termo crescente ou minguante refere-se à porção clara
(ou iluminada) que cresce ou descresce.
prof. Dulcidio Braz Júnior (@Dulcidio)