Borges e Nicolau
Isaac Newton, com base nas Leis de Kepler, descobriu que a força que mantém um planeta em órbita em torno do Sol tem intensidade diretamente proporcional à massa do Sol e à massa do planeta e inversamente proporcional ao quadrado da distância entre eles. Essas forças de interação à distância são denominadas forças gravitacionais. Vamos, a seguir, enunciar a Lei da Gravitação Universal para dois pontos materiais:
x
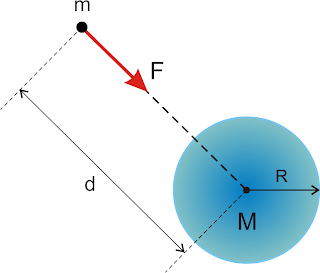
Dois pontos materiais de massas m e M e situados a uma distância d atraem-se com forças que têm a direção da reta que os une e cujas intensidades são diretamente proporcionais ao produto das massas e inversamente proporcional ao quadrado da distância que os separa.
G = 6,67 x 10-11 N.m2/(kg)2 é a constante de gravitação universal.
No caso de duas esferas homogêneas a distância a ser considerada, para a aplicação da Lei da Gravitação Universal, é entre os centros das esferas.
x
Aceleração da gravidade
x
Vamos considerar um ponto material de massa m situado a uma distância d do centro da Terra, suposta esférica, homogênea, estacionária e de massa M.
x
A intensidade da força de atração gravitacional F entre M e m é, nestas condições, o próprio peso P do ponto material. Assim, podemos escrever:
Velocidade de translação de um satélite em órbita circular
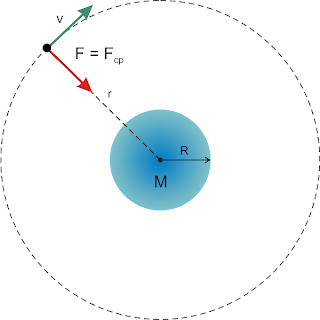
Um satélite de massa m descreve uma órbita circular de raio r, em torno de um planeta de massa M
Para determinar a velocidade de translação do satélite, basta observar que a força de atração gravitacional, que o planeta exerce no satélite, é a resultante centrípeta:
Observe que a velocidade de translação do satélite depende da massa M do planeta, do raio r da órbita e não depende da massa m do satélite. A força de atração gravitacional, que o planeta exerce no satélite e nos corpos situados no seu interior, está sendo usada como resultante centrípeta que tem, como única função, manter os corpos em órbita. Por isso, os corpos no interior dos satélites flutuam: é a chamada imponderabilidade.
Recorde a lei de Newton da Gravitação Universal pela animação abaixo:
Clique aqui
x
Exercícios básicos
Exercício 1:
Sejam M = 6,0.1024 kg e R = 6,4.106 m a massa e o raio da Terra. Uma pequena esfera de massa 10 kg está sobre a superfície da Terra. Qual é a intensidade da força de atração gravitacional que a Terra exerce na esfera? É dada a constante de gravitação universal: G = 6,67 x 10-11 N.m2/(kg)2
Exercício 2:
A força de atração gravitacional, entre duas pequenas esferas de massas m e M, situadas a uma distância d, tem intensidade F. Reduzindo-se à metade a distância entre as esferas, a intensidade da força de atração gravitacional passa a ser F’. Determine a razão F’/F.
x
Exercício 3:
Seja g = 10 m/s2 a intensidade da aceleração da gravidade na superfície da Terra, cujo raio é R. Num ponto situado à distância 2R do centro da Terra a aceleração da gravidade passa a ter intensidade:
a) 7,5 m/s2; b) 6,0 m/s2; c) 5,0 m/s2; d) 2,5 m/s2; e) 1,25 m/s2
x
Exercício 4:
Um corpo situado na superfície terrestre pesa 80 N. Qual seria o peso desse corpo se fosse colocado na superfície de Urano? Sabe-se que a massa de Urano é 14,6 vezes a massa da Terra e que seu raio é 4 vezes o raio da Terra.
x
Exercício 5:
Um planeta tem massa igual ao dobro da massa da Terra e raio igual à metade do raio da Terra. Seja g a aceleração da gravidade na superfície da Terra. Determine, em função de g, a aceleração da gravidade g’ na superfície do planeta.
Resolução: clique aqui
Exercício 6:
Dois satélites, A e B, estão emBórbita circular em torno da Terra. O raio da trajetória descrita por A é rA e o de B, é rB = 2.rA. Sejam vA e vB as velocidades de translação dos satélites e TA e TB seus períodos de translação. Determine as relações:
vA/vB e TA/TB?
Exercício 1: resolução
Exercício 2: resolução
De:
Exercício 3: resolução
Exercício 4: resolução
Exercício 5: resolução
Exercício 6: resolução
x















Nenhum comentário:
Postar um comentário